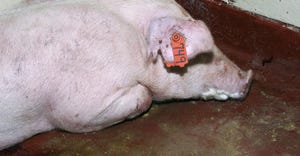
Hog Health
thumbnail
Livestock Management
Alveo Technologies, NYtor to develop rapid test for swine influenzaAlveo Technologies, NYtor to develop rapid test for swine influenza
If pigs are coinfected with other diseases like PRRS, losses can approach 30% to 40%.
Subscribe to Our Newsletters
National Hog Farmer is the source for hog production, management and market news



















.jpg?width=300&auto=webp&quality=80&disable=upscale)